1 f(x) = 1 c) lim x!0005 0050 0499 x approaches 0 from the left x approaches 0 from the right f x approaches 2 f x approaches 2 −1 1 1 x x f is undefined at x = 0 f(x) = x 1 − 1Jun 13, 21 · Use the graph to investigate the limit of f(x) as x tends to 0 Let me see I gotta use the graph to investigate the limit of f(x) as x tends to 0 from the left and right Let y = f(x) The given function can also be expressed as f(x) = x The limit of (x) as x>0
Calculus Limits
Lim x approaches infinity f(x)=0 graph
Lim x approaches infinity f(x)=0 graph-Condition Required for Existence of Limit of a Function lim x>x 0 f(x) = L exists if the following hold (i) lim x>x 0 f(x) exists, (ii) lim x>x 0 f(x) exists, and (iii) lim x>x 0 f(x) = lim x>x 0 f(x) = L Solved Problems Problem 1 Use the graph to find the limits (if it exists)Lim x!0 x 2 sin(1=x) = 0, since the graph of the function is sandwiched between y = x2 and y= x2 O x K 1 K 05 0 05 1 K 1 K 05 05 1 Example Calculate the limit lim x!0 x 2 sin 1 x We have 1 sin(1=x) 1 for all x, multiplying across by x2 (which is positive), we get x2 x 2sin(1=x) x for all x, Using the Sandwich theorem, we get 0 = lim x!0 x
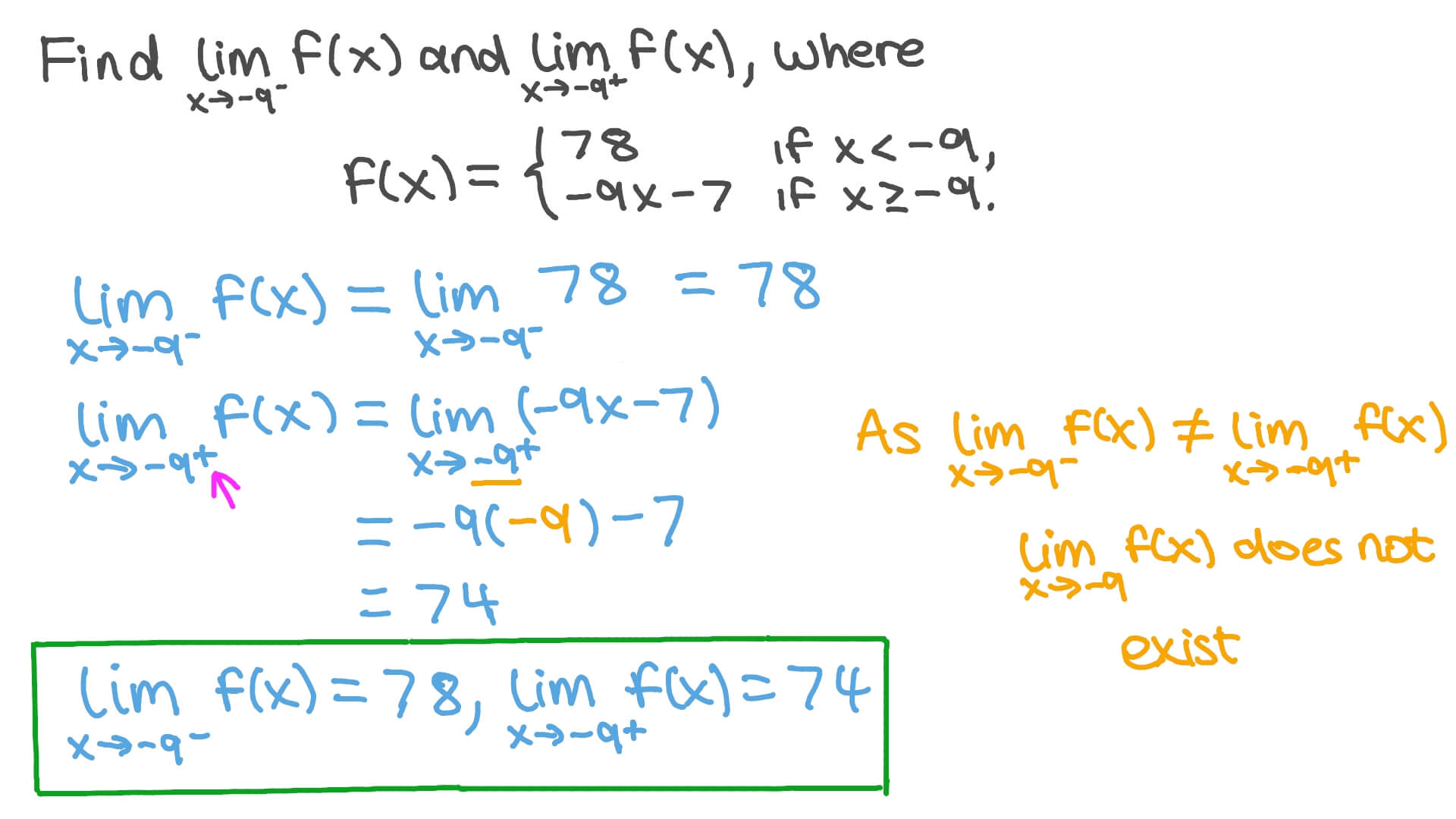



Question Video Finding The One Sided Limits Of A Piecewise Defined Function Nagwa
Since f(−x) = e− (− x) 2 2 = e− 2 = f(x) and lim x→±∞ e− (−x)2 2 = 0, the graph is symmetry wrt the yaxis, and the xaxis is a horizontal asymptote • Wehave f0(x) = e−x 2 2 (−x) = −xe− x2 2 • Thus f ↑ on (−∞,0) and ↓ on (0,∞) • Atx = 0, f 0(x) = 0 Thus f(0) = e = 1 is the (only) local andEvaluating a Limit Using a Table of Functional Values 1 Evaluate lim x → 0sinx x using a table of functional values Show Solution We have calculated the values of f ( x) = ( sin x) / x for the values of x listed in (Figure) Table of Functional Values for lim x → 0 sin x x xG(x) c) lim x→3 g(x) d) lim x→0 g(x) e) lim x→2 g(x) f) equations of the asymptotes Example Sketch the graph of an example of a function f that satisfies all of the following conditions a) lim x→2 f(x) = −∞ b) lim x→∞ f(x) = ∞ c) lim x→−∞ f(x) = 0 d) lim x→0 f(x) = ∞ e) lim x→0− f(x) = −∞ Example Find
Overall Limit lim x → 2 f ( x) = 05 Let's find the limits in a couple examples Example 1 Sketch a graph and create a table to determine the limit of the function as x → 2 lim x → 2 x − 1 3 x Step 1 Graph the function Step 2 Create a table of values close to and on either side of 2 x1 f(x) =DNE d) lim x!0 f(x) = 2 e) lim x!0 f(x) = 2 f) lim x!0 f(x) = 2 g) lim x!2 f(x) = 2 h) lim x!2 f(x) = 1 i) lim x!2 f(x) =DNE 2 Evaluate the following limit usingLim F X 0 Graph príprava na vyučovaciu hodinu slovenského jazyka 7 ročník príkazná zmluva a odvody 19 príklady z matematiky pre 1 ročník z Find Lim F X As X Approaches 0 If It Exists Study Com For more information and source, see on this link https
Ex 0 10 100 1000 lim 3 2 = − →∞ x x x x The limit as x → −∞ is the same The graph of the function in the limit above has a horizontal asymptote y = 0The xaxis goes from negative 3 to 3 The graph is a Ushaped curve that starts at about (negative 25, 4), moves downward to an open circle at (0, 1), moves upward, and ends at about (25, 4) This is the graph of y = x / sin (x) Notice that there's a hole at x = 0 because the function is undefined there In this example, the limit appears toThis calculus video tutorial explains how to evaluate limits from a graph It explains how to evaluate one sided limits as well as how to evaluate the funct




Sketch The Graph Of A Function That Satisfies All Of Chegg Com




Sketch The Graph Of An Example Of A Function F That Satisfies All Of The Given Conditions Lim F X Oo Lim F X Oo Lim F X Oo Lim F X
Graph the rational function exists x33x216x48 x22x3 Find all intercepts and asymptotes Then state the value of the limit, if it xintercept(s)Lim_(x>0)(3x1)=1 Basically, as a general rule, when you have to evaluate a limit for xMar 14, 17 · If $\lim_{x\to a} f(x) = 0$ then $\lim_{x\to a}f(x) = 0$ This is the limit property that we have been given Now, why can't we say If $\lim_{x\to a}f(x) = 0$ then $\lim_{x\to a}f(x) = 0$ I can't think of any graphs I know of that would make the above false Can anybody explain why this only works one way?



Solved Explain Each Condition And Sketch The Graph Of A Function That Satisfies All Of The Following Conditions F 0 0 Lim F X Infinity As X Ap Course Hero




Limits Of Combined Functions Video Khan Academy
Apr 12, 18 · (Mathematicians frequently abbreviate "does not exist" as DNE Thus, we would write \(\displaystyle \lim_{x \to 0} \sin(1/x)\) DNE) The graph of \(f(x)=\sin(1/x)\) is shown in Figure \(\PageIndex{6}\) and it gives a clearer picture of the behavior of \(\sin(1/x)\) as \(x\) approaches \(0At x=0, f(x) doesn't have any specific value on the graph When this happens, we say that f(x) increases without bound as x approaches c Every time this happens with a limit, we can simply write that the limit does not exist because f(x) does not approach any fixed, finite value as x approaches c However, that is a little unwieldy to write, so instead mathematicians haveX 0, f(x) f f x xlim x→0 x x 1 f x x x 1 1 x 12 Finding Limits Graphically and Numerically 49 x 001 0001 0 0001 001 f x ?
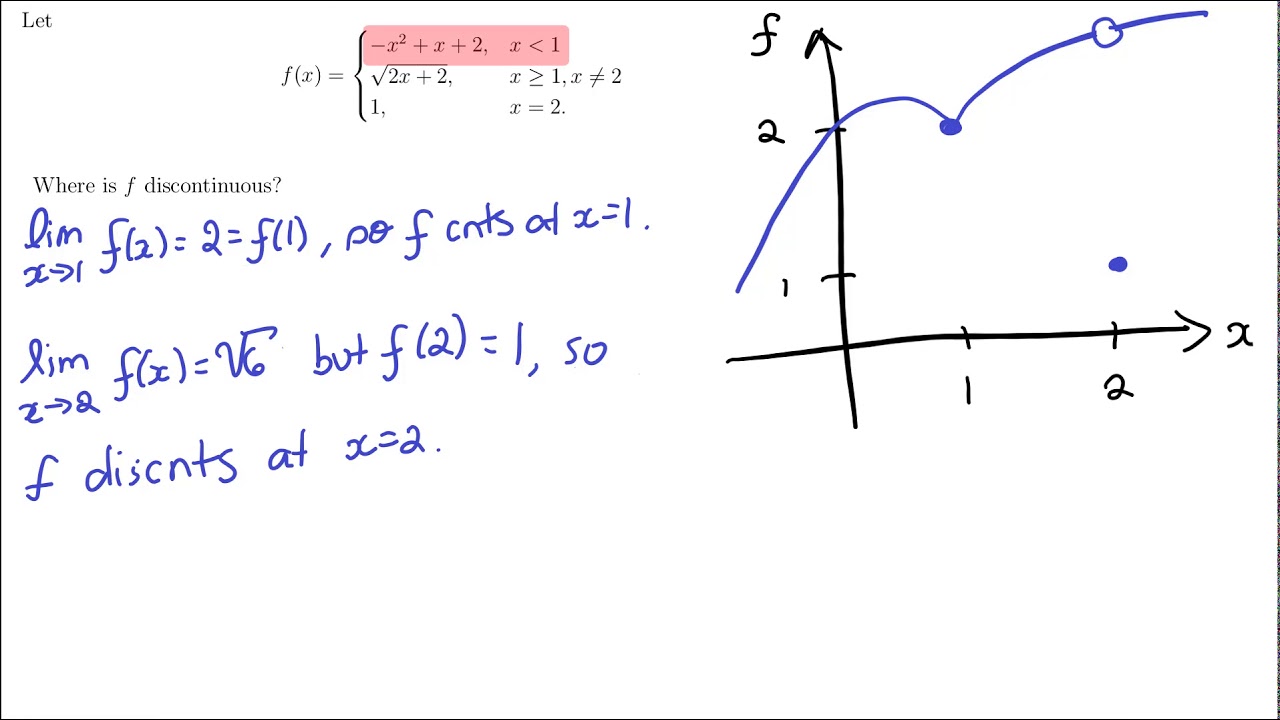



Continuity And Ivt




Plot The Graph Of The Function F X Lim T 0 2x Pitan 1 X
From the graph of f (x), f (x), we observe the output can get infinitesimally close to L = 8 L = 8 as x x approaches 7 from the left and as x x approaches 7 from the right To indicate the lefthand limit, we write lim x → 0 − f (x)Get stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!6lim x!af(x)n = lim x!a f(x) n, where nis a positive integer (we see this using rule 4 repeatedly) 7lim x!a c= c, where c is a constant ( easy to prove and easy to see from the graph, y= c) 8lim x!a x= a, (not di cult to prove from the de nition and easy to see from the graph, y= x) 9lim x!1 1 x = 0 10lim x!a n p f(x) = n p lim x!a f(x) assuming that the lim x!a f(x) >0 if nis even



Solved The Graph Of Fis Given Use The Graph To Compute The Quantities Asked For If A 2 Y A Xinlzx B Lim F X X0 Course Hero
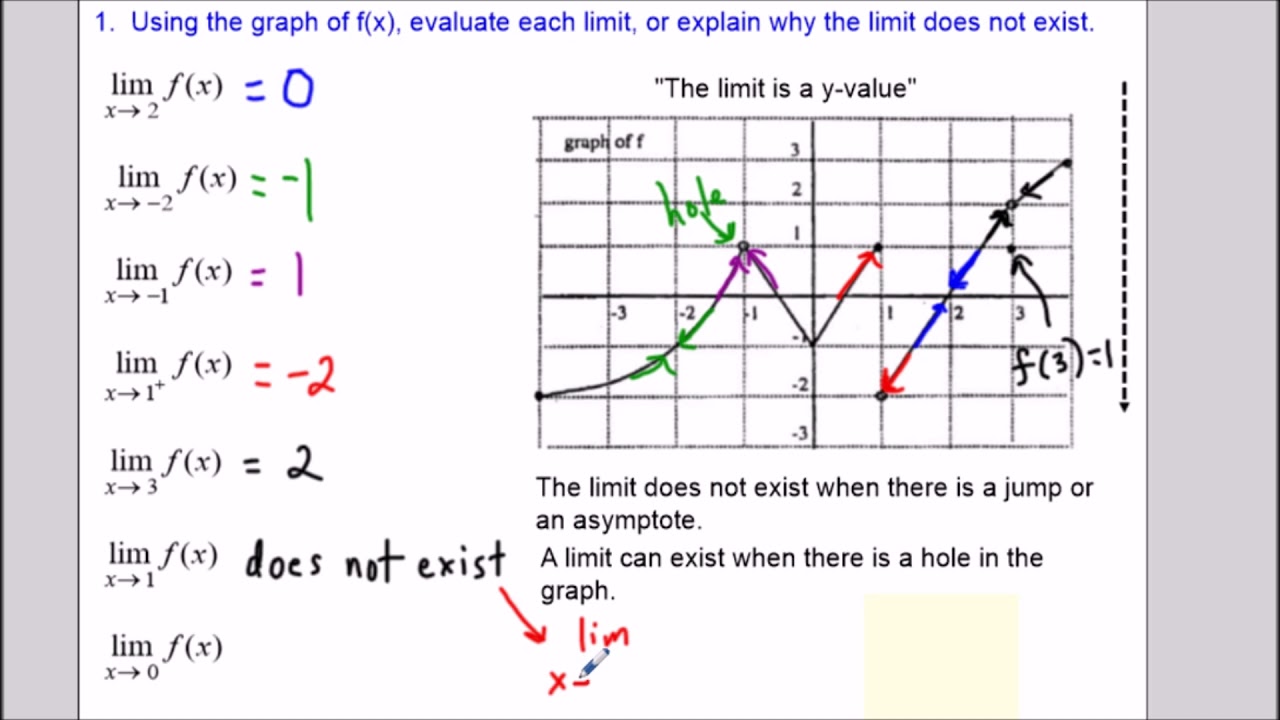



Determining Limits And Continuity From A Graph Ap Calculus Youtube
Sep 16, 14 · Given that $$\lim_{x \to 0} \frac{f(x)}{x^2}=6$$ evaluate the following limits a) $\displaystyle\lim_{x \to 0} f(x)$ b) $\displaystyle\lim_{x \to 0} \frac{f(x)}{x}$ I'm not quite sure where to even start here if someone could help me out I would appreciate itThe limit as x approaches 0 for f(x) does not exist (DNE) as the limit from the left does not match the limit from the right Test for Continuity Rule 1 f(1) exists We can see that f(0) equals 1, so f(0) exists Rule 2 The limit as x approaches 1 from the left must equal the limit as x approaches 1 from the rightAnswer lim x → ∞ f ( x) ≈ 3 lim x → − ∞ f ( x) ≈ 0 Advertisement Example 3 Use the table below to estimate lim x → − ∞ f ( x) x f ( x) − 10 85 − 50 81 − 100 8013 − 1000 − − The larger x gets in the negative direction, the closer the function seems to get to 8 Answer
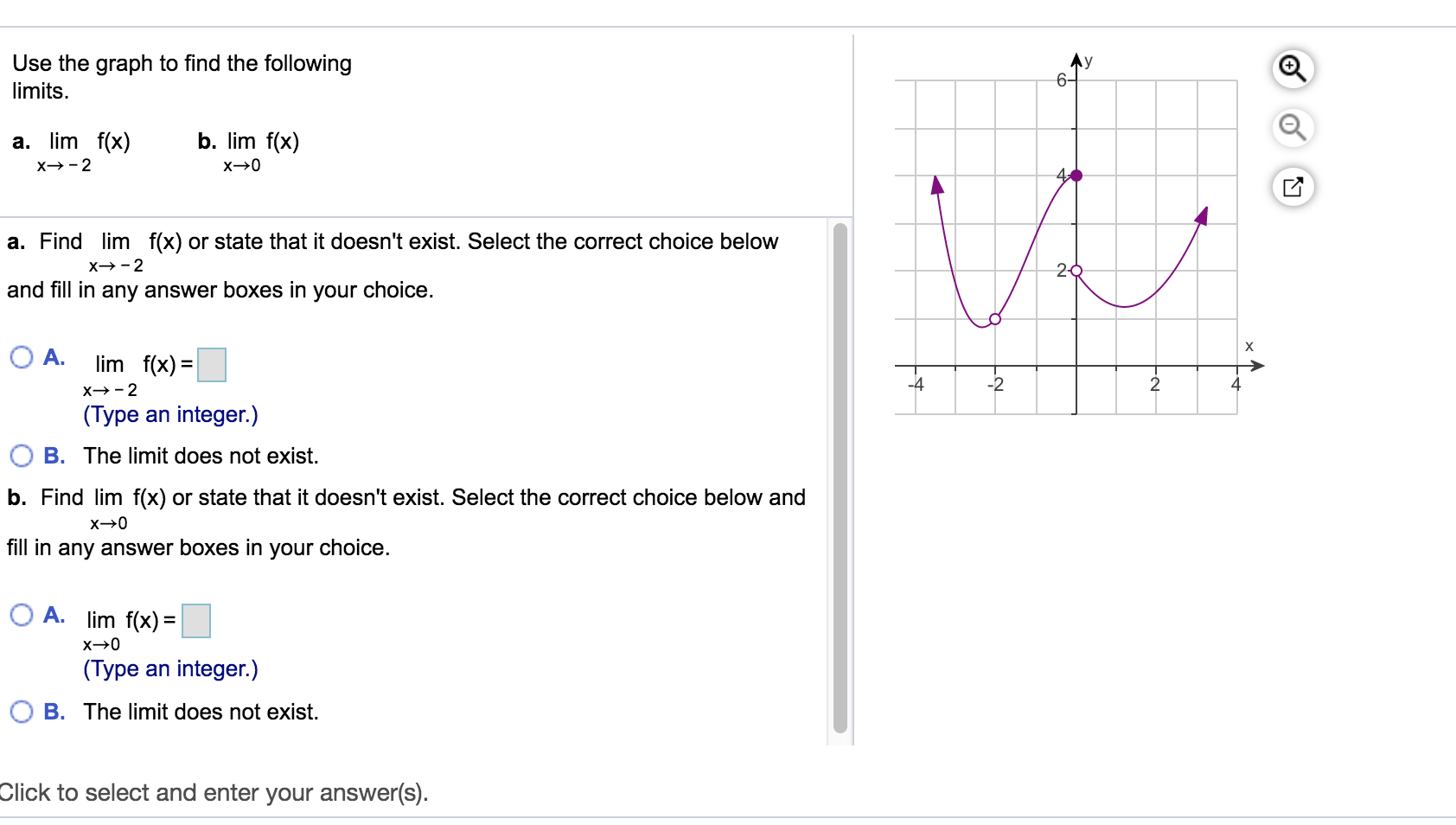



Solved Use The Graph To Find The Following Limits O O A Chegg Com




Taller Calculo Diferencial Trigonometric Functions Mathematical Analysis
Solve limits stepbystep \square!F ( x) Move the term F F outside of the limit because it is constant with respect to x x F lim x→6x F lim x → 6 x Evaluate the limit of x x by plugging in 6 6 for x x F ⋅6 F ⋅ 6 Move 6 6 to the left of F F 6F 6 FJun 16, 21 · For the functions in exercises 28 30, use f ″ (x) = lim h → 0 f′ (x h) − f′ (x) h to find f ″ (x) For exercises 31 36, use a calculator to graph f(x) Determine the function f′ (x), then use a calculator to graph f′ (x) 32) T f(x) = 3x2 2x 4
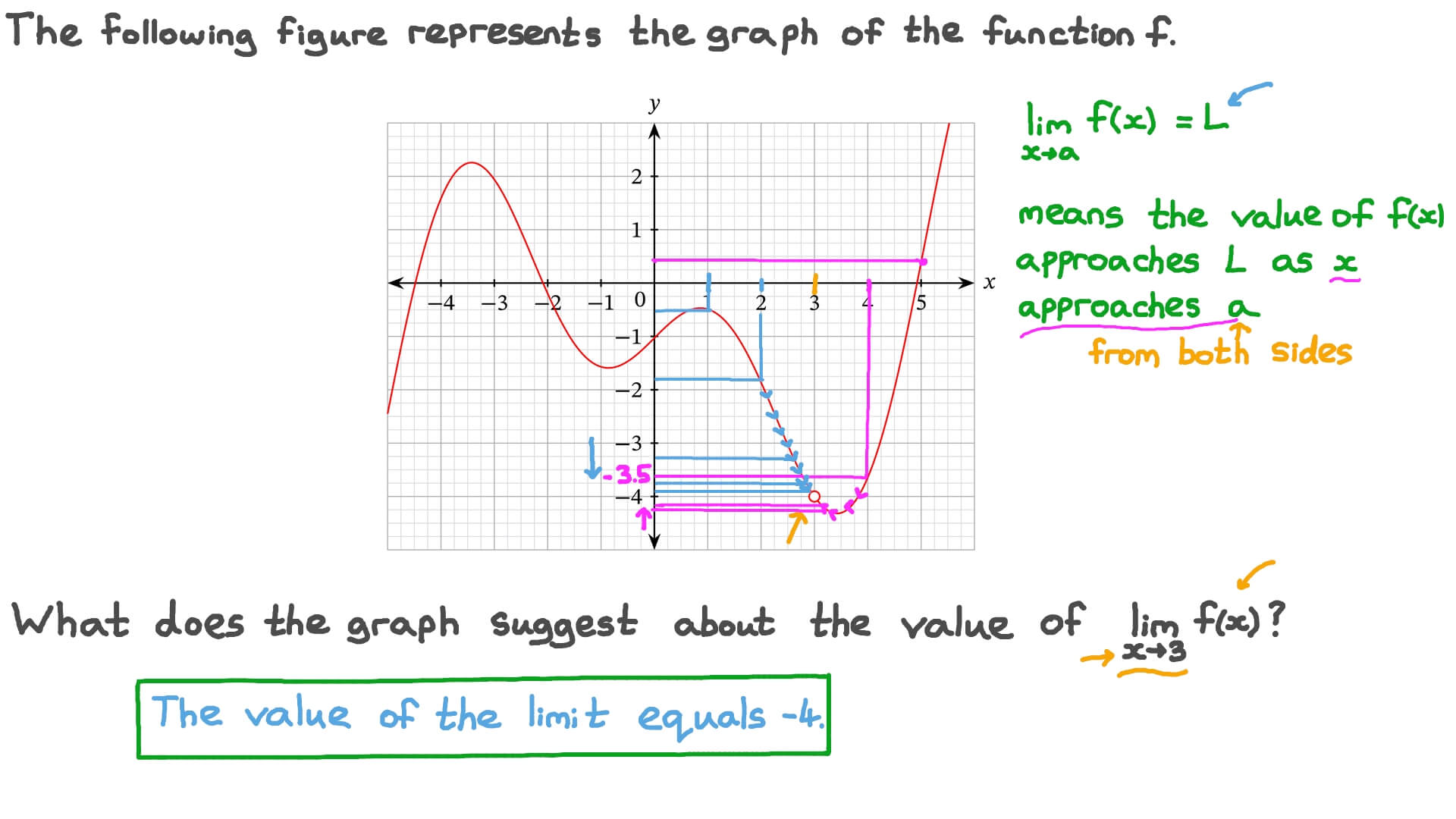



Question Video Finding The Value Of A Limit From A Graph Nagwa
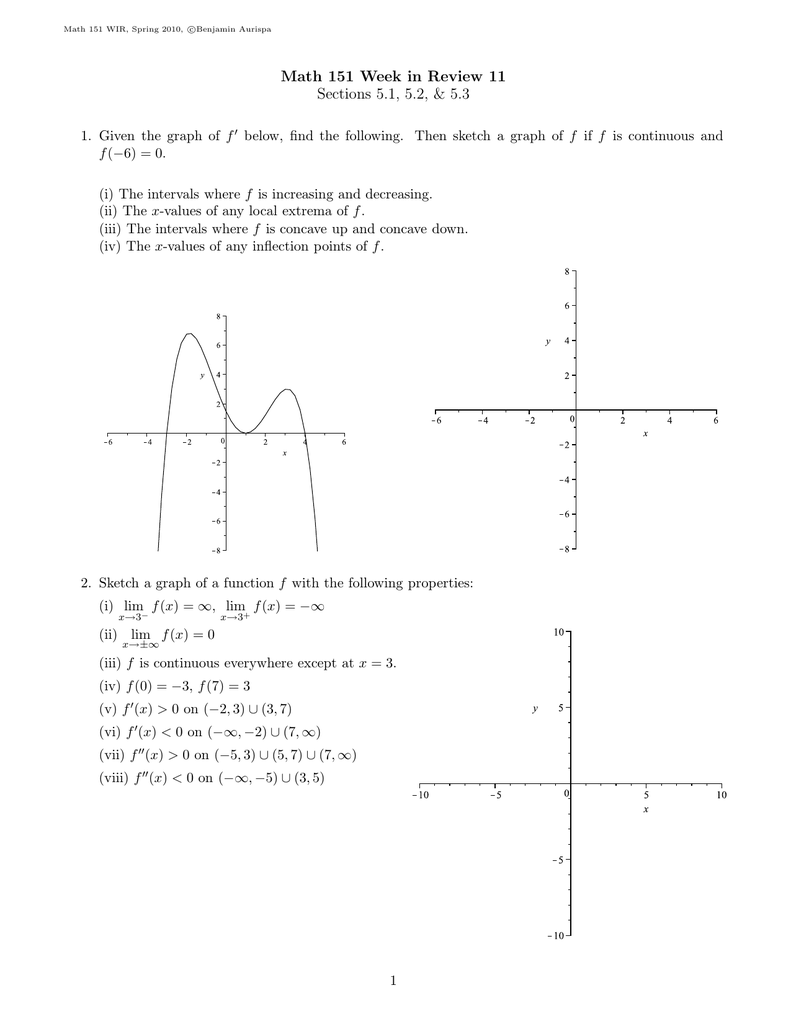



Document
1 f(x) = 1 b) lim x!May 01, 17 · Graph of f 77 The figure above shows the graph of a function f with domain 0 x 4 Which of the following statements are true?Answers 1 Get Other questions on the subject Mathematics Mathematics, 1400, ira51 Can you decompose the numbers ,740,6,000 Answers 1 continue Mathematics, 1840, scadengo123 What is the yintercept of the function, represented by the table of values



Calculus Limits
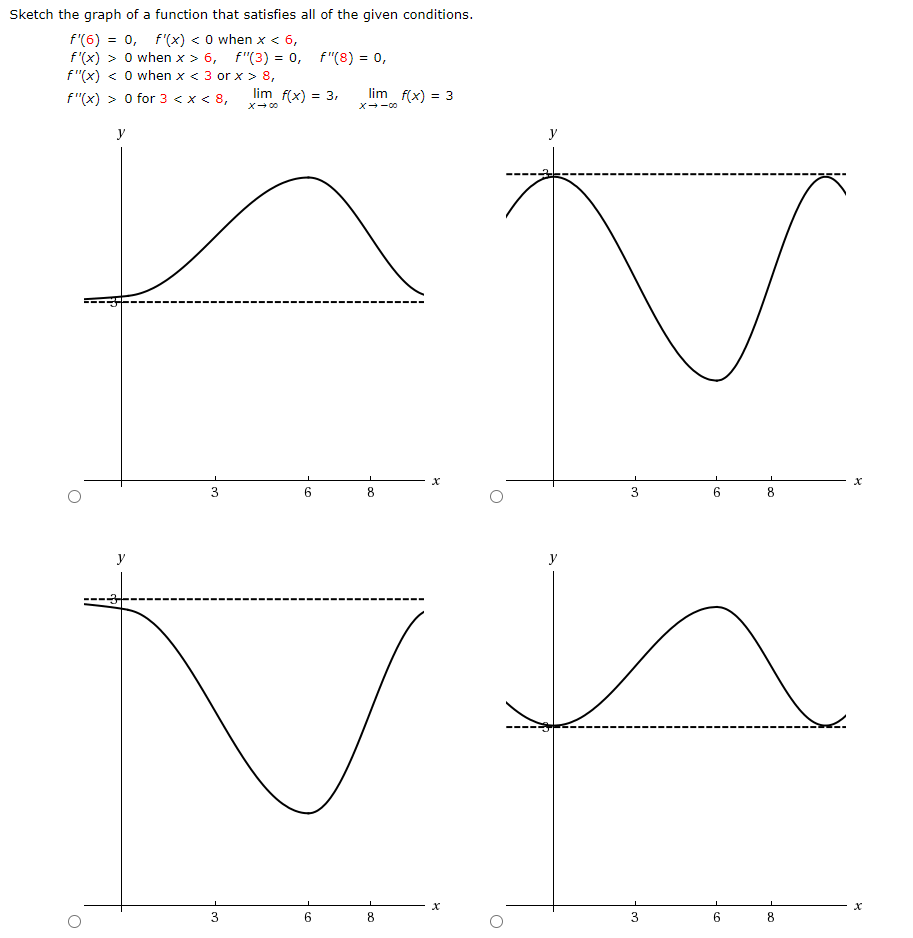



Solved Sketch The Graph Of A Function That Satisfies All Chegg Com
(Mathematicians frequently abbreviate "does not exist" as DNE Thus, we would write lim x → 0 sin (1 / x) lim x → 0 sin (1 / x) DNE) The graph of f (x) = sin (1 / x) f (x) = sin (1 / x) is shown in Figure 217 and it gives a clearer picture of the behavior of sin (1 / x) sin (1 / x) as x approaches 0I lim f (E) exists IIS lim f (x) f(x) exists (B) 11 only (A) I only only (D) f(2) (E) 1, 11, and 79 Let f be a function such that lim I, f is continuous at x = 2 Il f is differentiable at x = 2Sketch the graph of a function f that satisfies the given values f(0) is undefined lim x > 0 f(x) = 4 f(2) = 6 lim x > 2 f(x) = 3 Solution From the given question, We understood that the functions is undefined when x = 0 When the value of x approaches 0 from left hand side and right hand side, limit value will approaches to 4
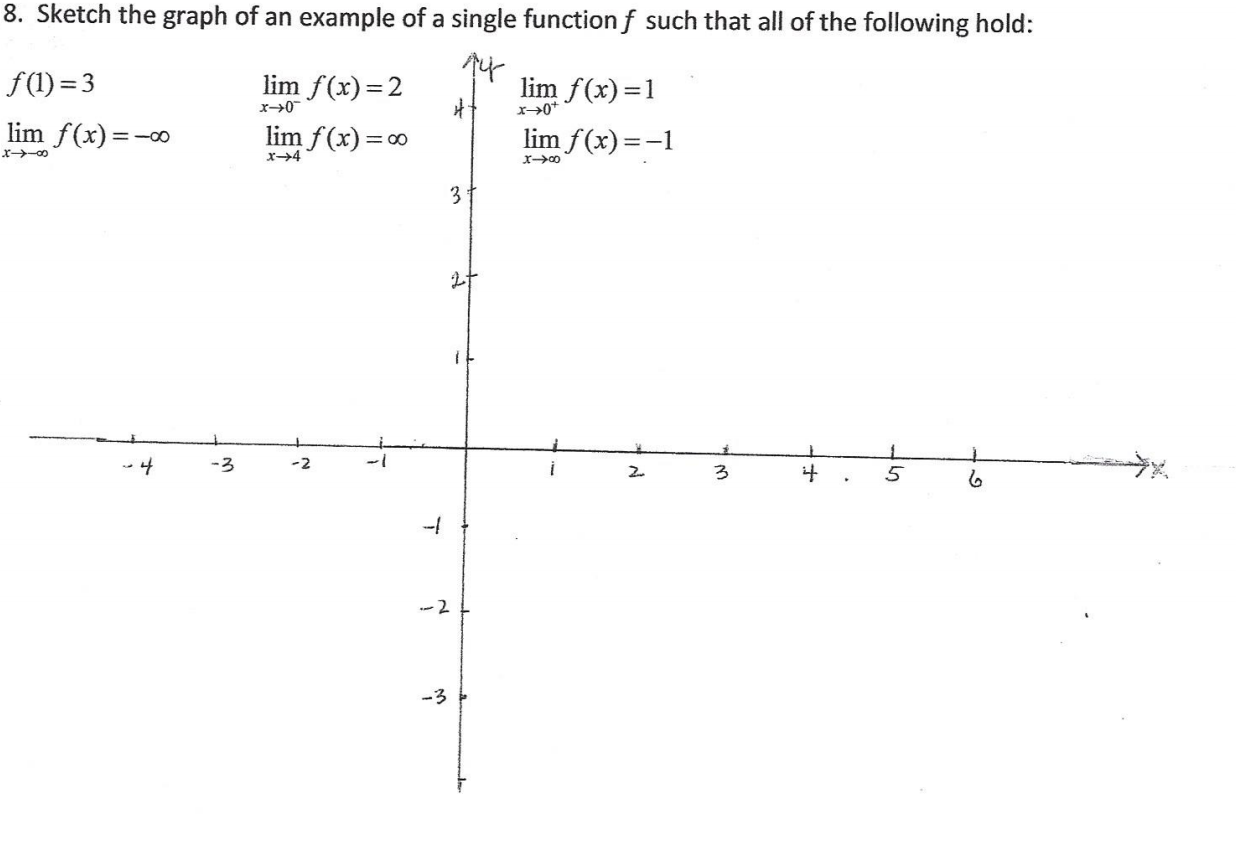



Answered E Sketch The Graph Of An Example Of A Bartleby




Which One Of The Following Best Represents The Graph Of The Functi
Aug 15, 16 · LIM‑1D2 (EK) Suppose we are looking for the limit of the composite function f (g (x)) at x=a This limit would be equal to the value of f (L), where L is the limit of g (x) at x=a, under two conditions First, that the limit of g (x) at x=a exists (and if so, let's say it equals L) Second, that f is continuous at x=LThe domain of the function is all real numbers except x = 4 and x = 0 Use the graph to evaluate the following a () 4 lim x f x → = 5 b () 0 lim x f x → = 2 c () 2 lim x f x →− = 3 d () 3 lim x f x → = DNE e () 3 lim x f x → − = 1 f () 3 lim x f x → = 4 g () 4 lim x f x →− = DNE h () 4 lim x f x →− − = DNE (or, more descriptively, ∞) Vertical asymptote i () 4 lim x f x →−Use the graph to estimate lim x → − 3 f ( x) Step 1 Examine the limit from the left Step 2 Examine the limit from the right Step 3 The onesided limits are the same, so the limit exists Answer lim x → − 3 f ( x) ≈ 2 Example 3



Epsilon Delta Definition Of A Limit Brilliant Math Science Wiki
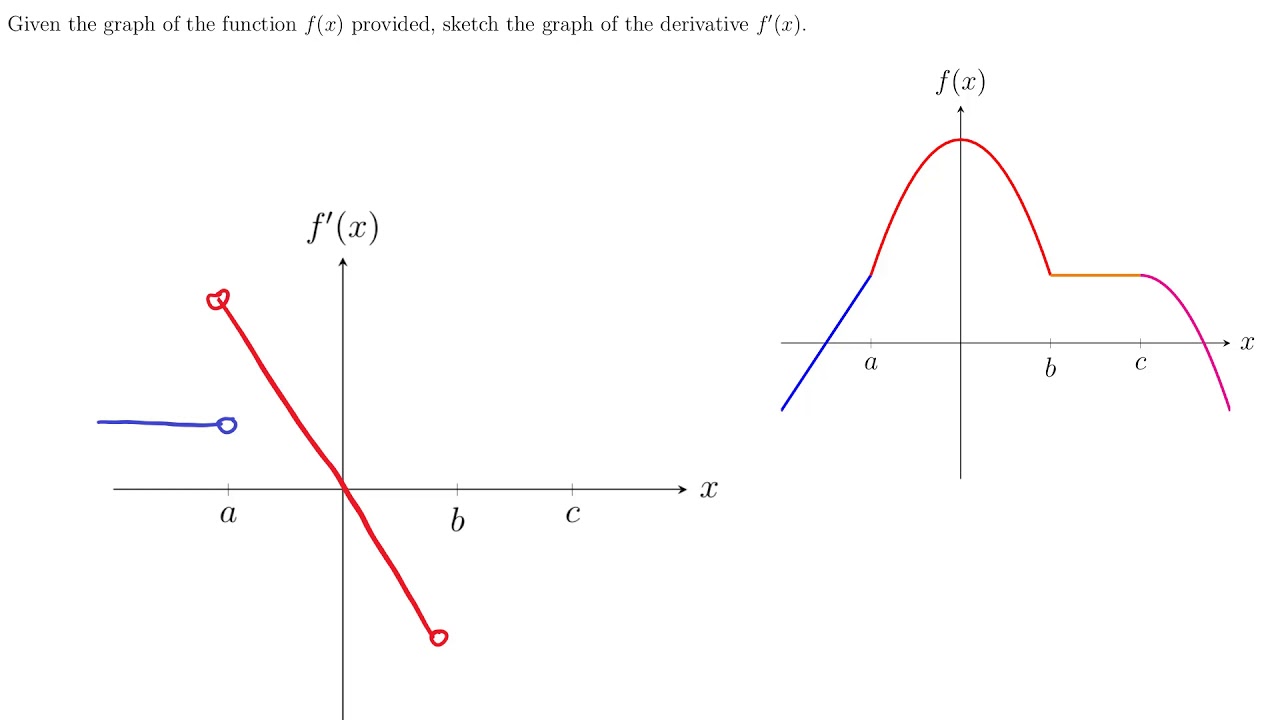



The Derivative Function
The graph of a function y= f(x) is shown below Determine the following limits or state that the limit does not exist a) lim x!F0(a) = dy dx x=a = lim h!0 f(a h) f(a) h Geometrically This is the slope of the tangent line to y= f(x) at x= a The equation of the tangent line to y= f(x) at the point (a;f(a)) is (from PointSlope Formula) y f(a) = m(x a) We now know that m= f0(a) Derivatives as Functions We can talk about the derivative at any point x f0(x) = dy dxAnswer to 16 Sketch the graph of a function f(x) that Math;
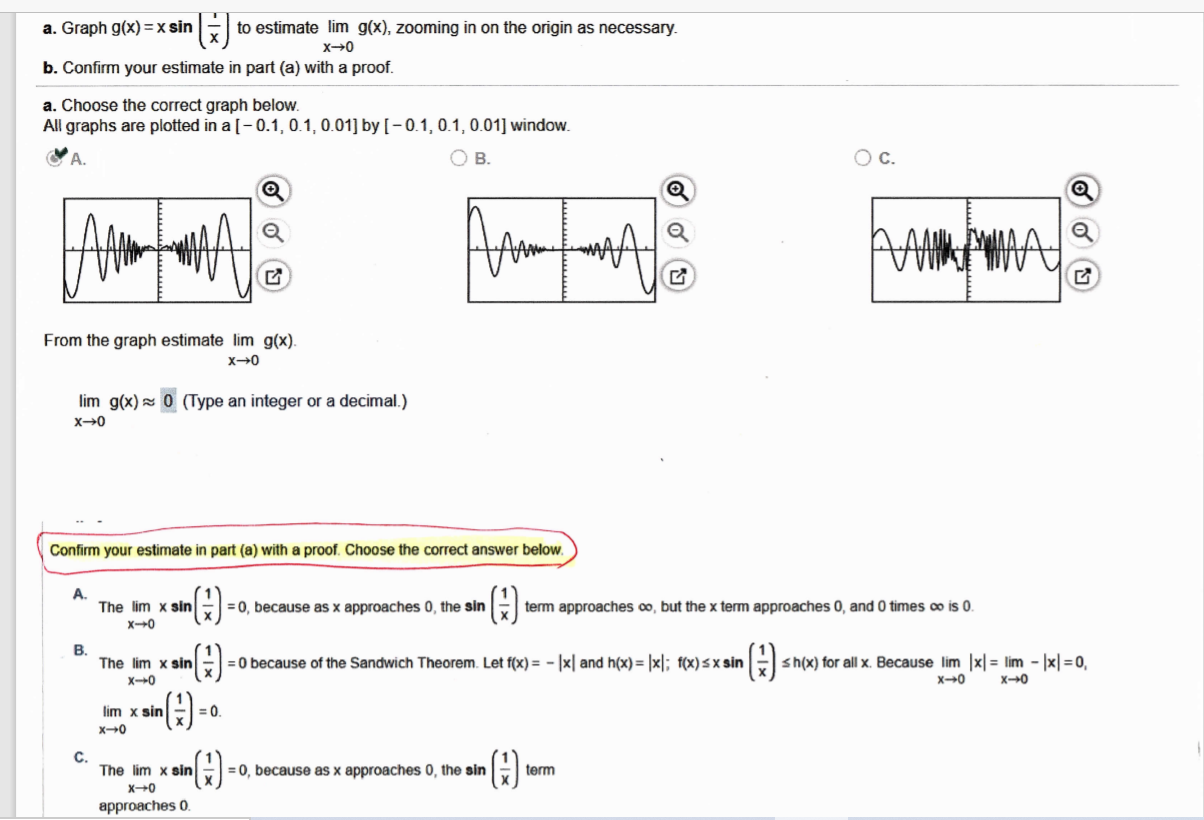



Answered A Graph G X X Sin To Estimate Lim Bartleby




What Would Lim X 0 X 0 X 0 And F 0 Be The Is Acting As A Limit Arrow Askmath
9 rows · Note that the left and right hand limits are equal and we cvan write lim x→0 f (x) = 1Jul 24, 15 · If you try to get near zero from the left (see the little sign over the zero) lim_(x>0^)1/x=oo this means that the value of your function as you approach zero becomes enormous but negative (try using x=001 or x=) 2 f(x)=3x1 as you approach zero from the right or left your function tends to 1!16 Sketch the graph of a function f(x) that satisfies all the following conditions a) lim f(x)=0, lim f (x) = 3, lim f(x)=3 10 b) lim f(x) = lim f(x)= 0 lim f(x) = 5




The Derivative



Solved The Following Graph Of The Function F Sati
48 Care with graphing The figure shows the graph of the function f 501x2 = 00 100x2 graphed in the window 34, 44 * 30, 4 a Evaluate lim xS0 S f 1x2, lim x 0S f 1 x2, and lim x 0 f 1 x2 T b Create a graph that gives a more complete representation of f 4 2 0 2 4 x 15 10 5 y 00 50 100 x 2 y Technology Exercises 49–56Jun 16, 21 · Use the graph to investigate the limit of f (x) as x tends to c at the number c See attachments Based on the graph of f (x), here is what I did lim (2x 1) as x tends to 0 from the left is 1 lim (2x) as x tends to 0 from the right is 0 LHL does not equal RHL I conclude the limit of f (x) as x tends to c at the number c (c = 0) does not existJun 21, 19 · Using the following graph, what is the lim x—> 0 f(x) ?



Calculus Limit Function Take The Limit As X Approaches




How To Read Limits From Graph Of Piecewise Function Mcv4u Youtube
Calculus Evaluate limit as x approaches 1 of f (x) lim x→1 f (x) lim x → 1 f ( x) Evaluate the limit of f (x) f ( x) which is constant as x x approaches 1 1F(x) = 1 (x 2)2 f has a vertical assymptote at x = 2 So f(x) can be made arbitrarily large by choosing x values very close to to x = 2 Hence f satisfies BADLIM #1 However, by the true definition lim x!1f(x) , 1(in fact the limit is zero) This is because taking arbitrarily large values of x does not yield arbitrarily large values of f(x) ForCalculus questions and answers;



4a Supplementary Problem 1 Let F Be The Function Dened On The Interval 0 2 By 2 Ifosxsl Fog 4 If1 Lt G2 The Graph Of Y F 1 Is Shown Course Hero
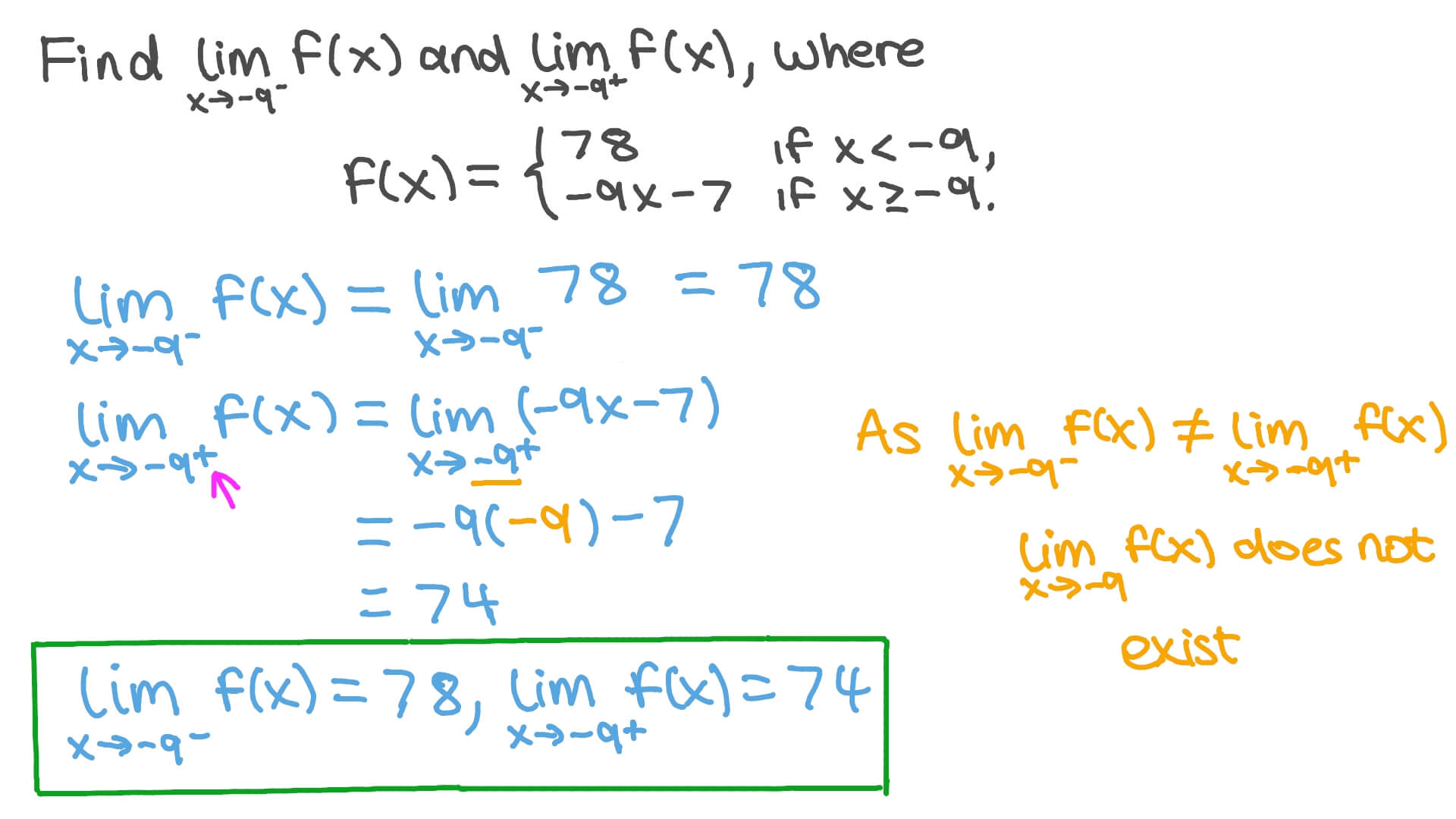



Question Video Finding The One Sided Limits Of A Piecewise Defined Function Nagwa
Solution to Example 4 Let r (x) = f (x) / g (x), where f (x) = 3 x and g (x) = x and apply theorem 4 above lim x→3 r (x) = lim x→3 (3 x) / lim x→3 x 3 x is the difference of two basic functions and x is also a basic function lim x→3 (3 x) = 3 3 = 0 and lim x→3 x = 3 Hence, lim x→3 r (x) = 0 / 3 = 0Oct 11, 14 · Psykolord19 Oct 11, 14 Given the function f (x) = 0, since this is a constant function (that is, for any value of x, f (x) = 0, the limit of the function as x → a, where a is any real number, is equal to 0 More specifically, as a constant function, f (x) maintains the same value for any x f (1) = f (2) = f (π) = f (e) = f ( − 44) = 0$$ \lim_{x \to 0}\frac{x}{\sqrt{1 3x} 1} $$ by graphing the function $ f(x) = x/(\sqrt{1 3x} 1) $ (b) Make a table of values of $ f(x) $ for $ x $ close to 0 and guess the value of the limit (c) Use the Limit Laws to prove that your guess is correct
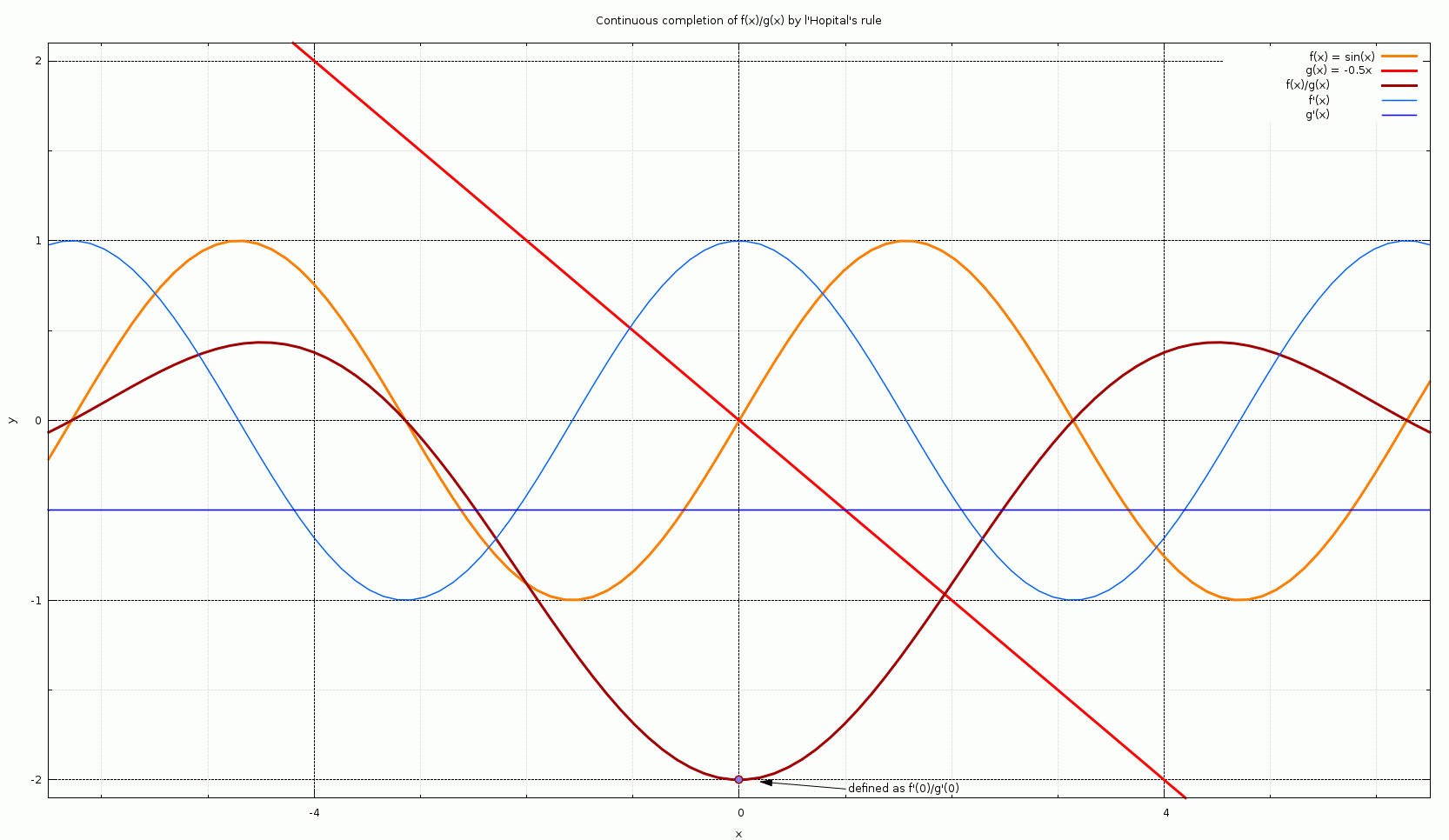



L Hopital S Rule Wikipedia




Which Statement Identifies And Explains Limit Of F X As X Approaches 0 Brainly Com
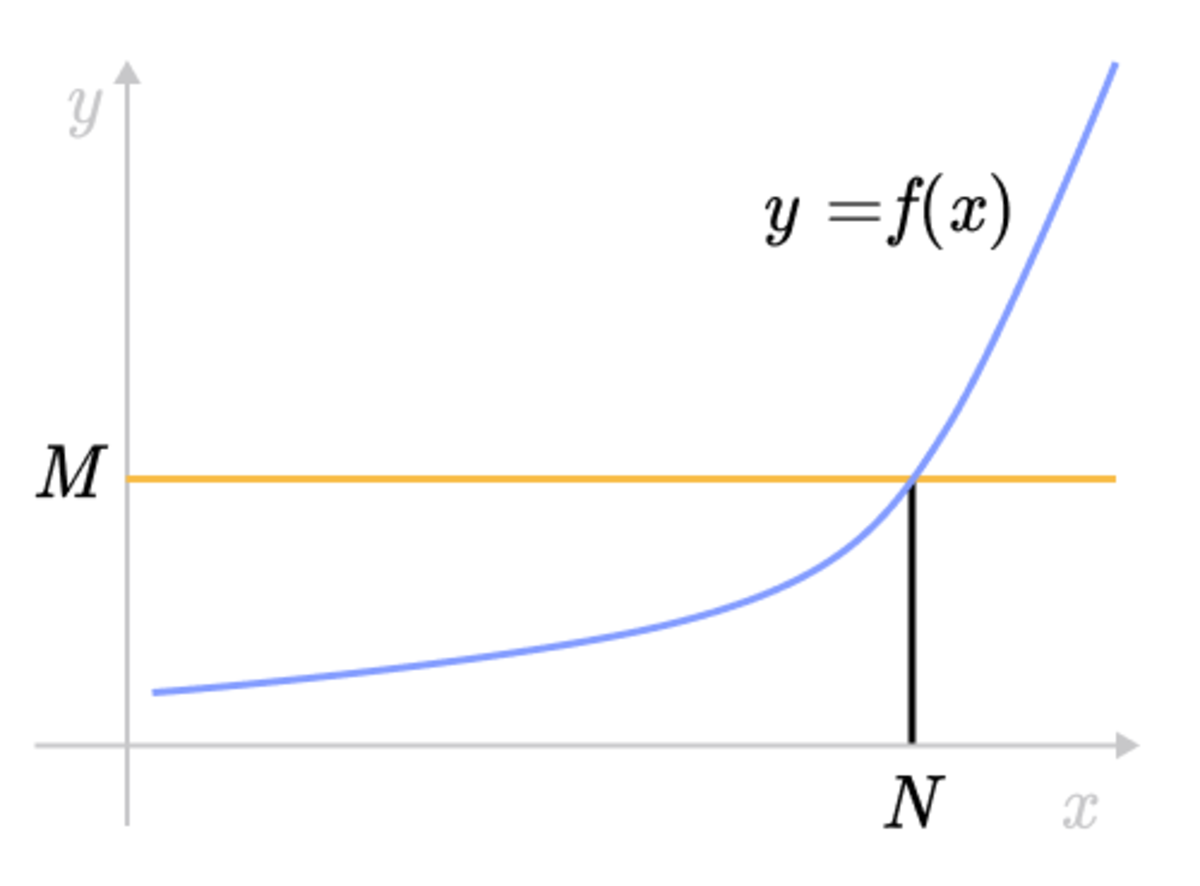
Then f x L x = →−∞ lim ( ) if for every ε > 0 there is a corresponding number N such that if x < N then ( ) f x L − < ε Definition What this can look like Horizontal Asymptote The line horizontal asymptotey = L is a of the curve y = f(x) if either is true 1 f x L x = →∞ lim ( ) or 2 f x L x = →−∞ lim ( ) Vertical Asymptote The line x = a is aExample 9 Analyze the limit lim x→0 2 √ x Be sure to graph the functions in each of the last three examples, and notice the graphs have vertical asymptotes at x =1,x=1, and x =0,respectively 24 University Of Kentucky > Elementary Calculus and its 5/10 Chapter3pdf (5/10)Lecture 1 1801 Fall 06 y x x 0 Figure 3 1Graph of x Hence, f (x 0) = − 2 1 x 0 Notice that f (x 0) is negative — as is the slope of the tangent line on the graph above Finding the tangent line Write the equation for the tangent line at the point (x




14 2 Limits And Continuity




Solved Use The Graph To Evaluate The Limit Lim X Tends T Chegg Com
Free functions calculator explore function domain, range, intercepts, extreme points and asymptotes stepbystep
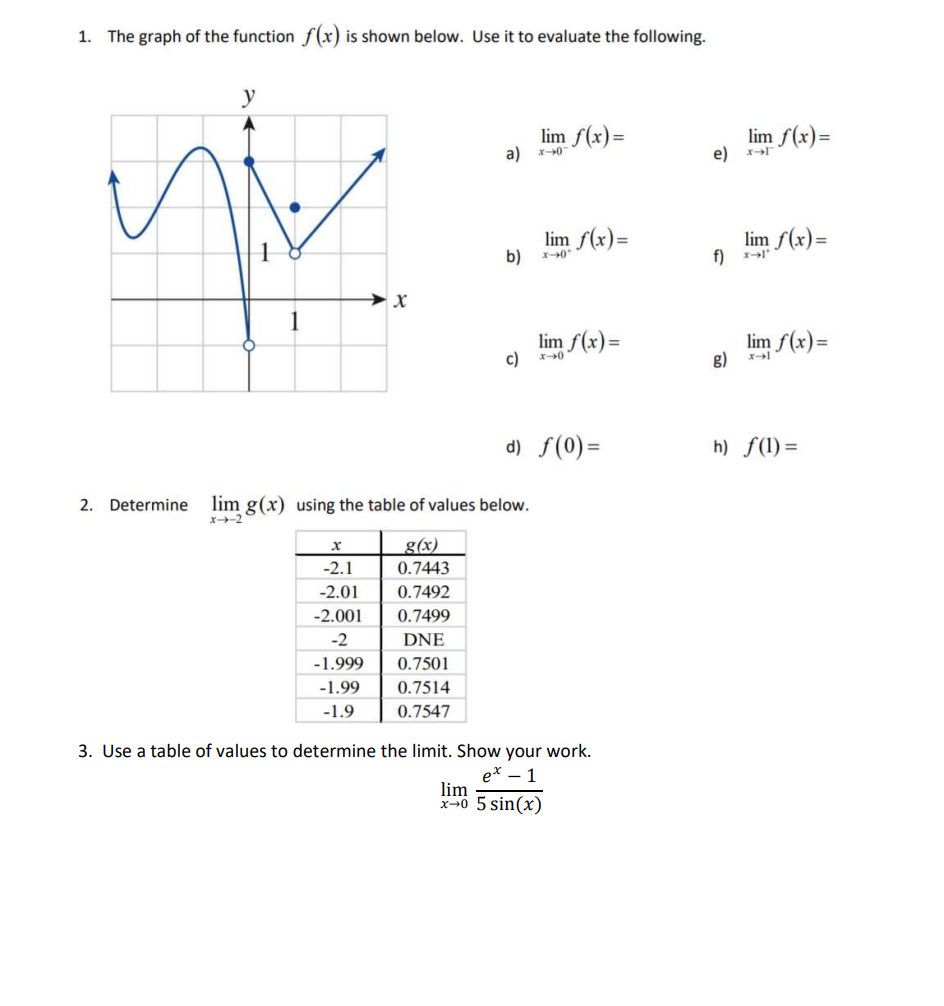



1 The Graph Of The Function F X Is Shown Below Use Chegg Com




Introduction To Limits At Infinity Video Khan Academy



Solved The Same Screen 36 Use The Squeeze Theorem To Show That A Find Lim 1 F X And Lim Lim Vx3 X2 Sin Quot 0 B Does Lim 1 F X Course Hero
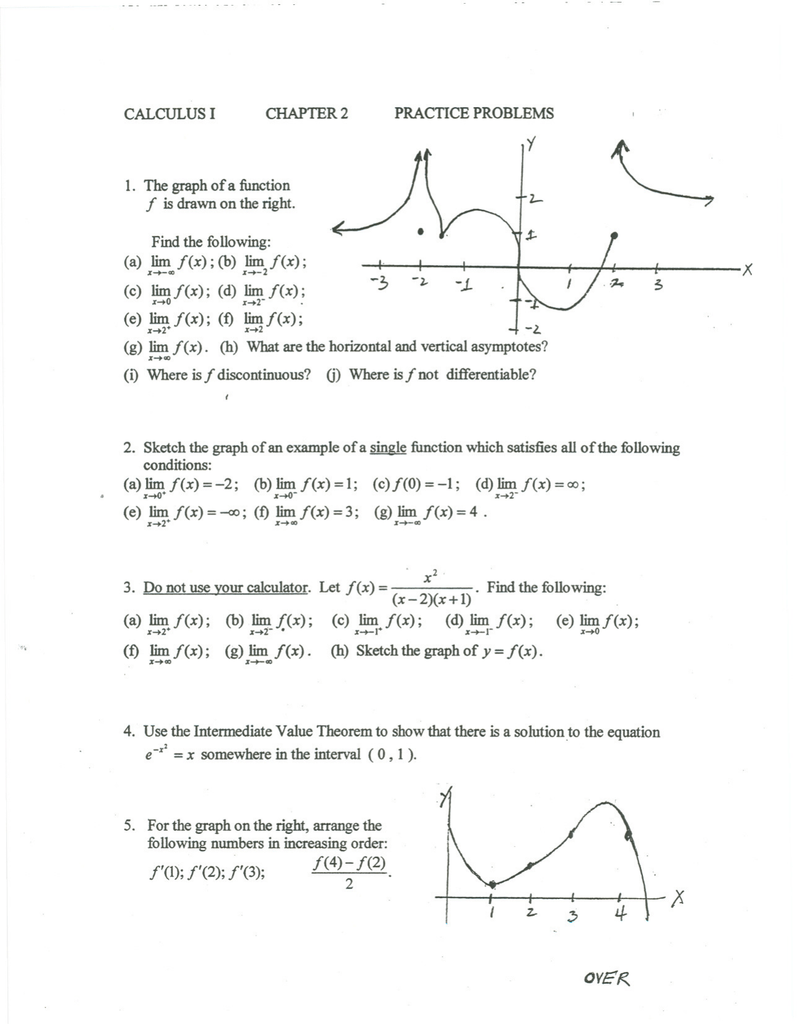



Free Essays Homework Help Flashcards Research Papers Book Reports Term Papers History Science Politics
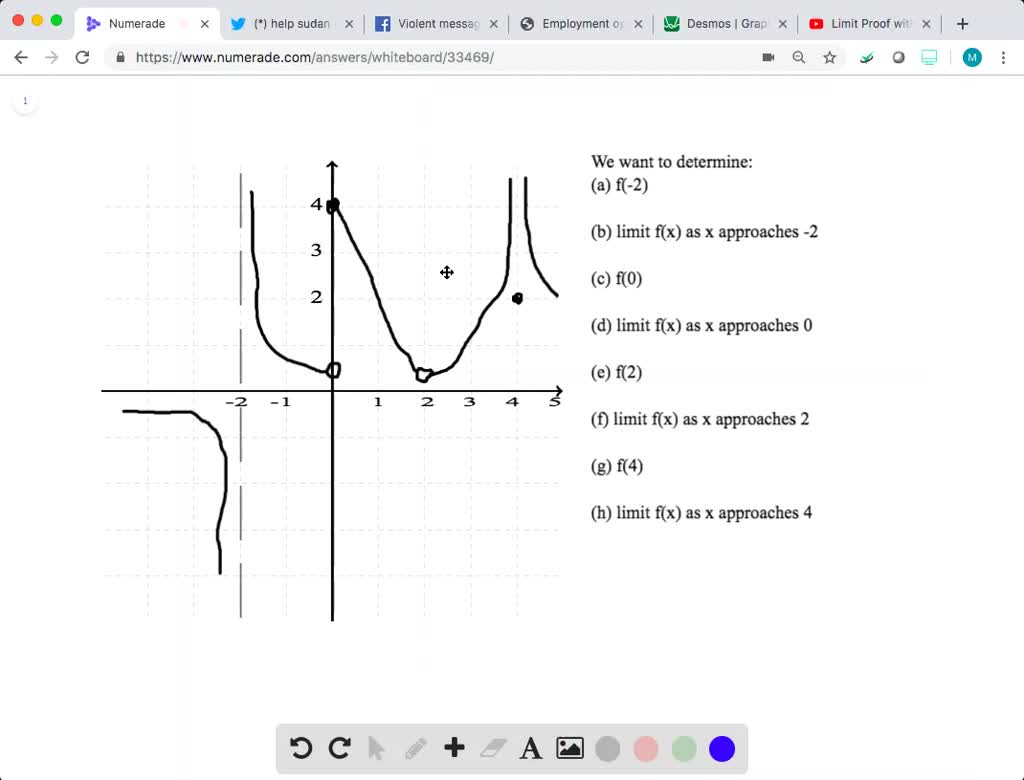



Solved Graphical Reasoning In Exercises 29 And 30
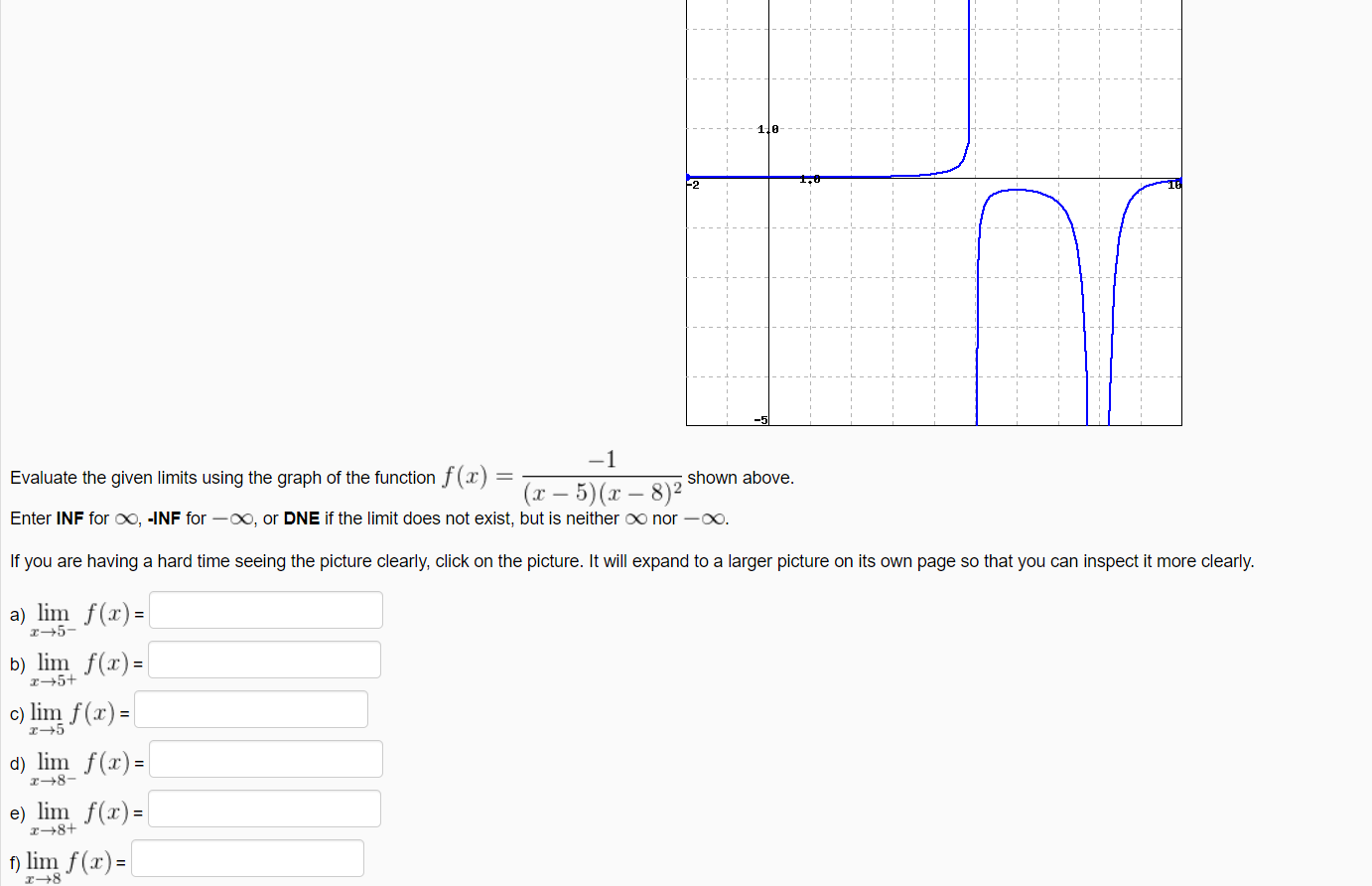



Answered 1 0 1 Evaluate The Given Limits Using Bartleby




How Do I Even Graph Limits Calculus
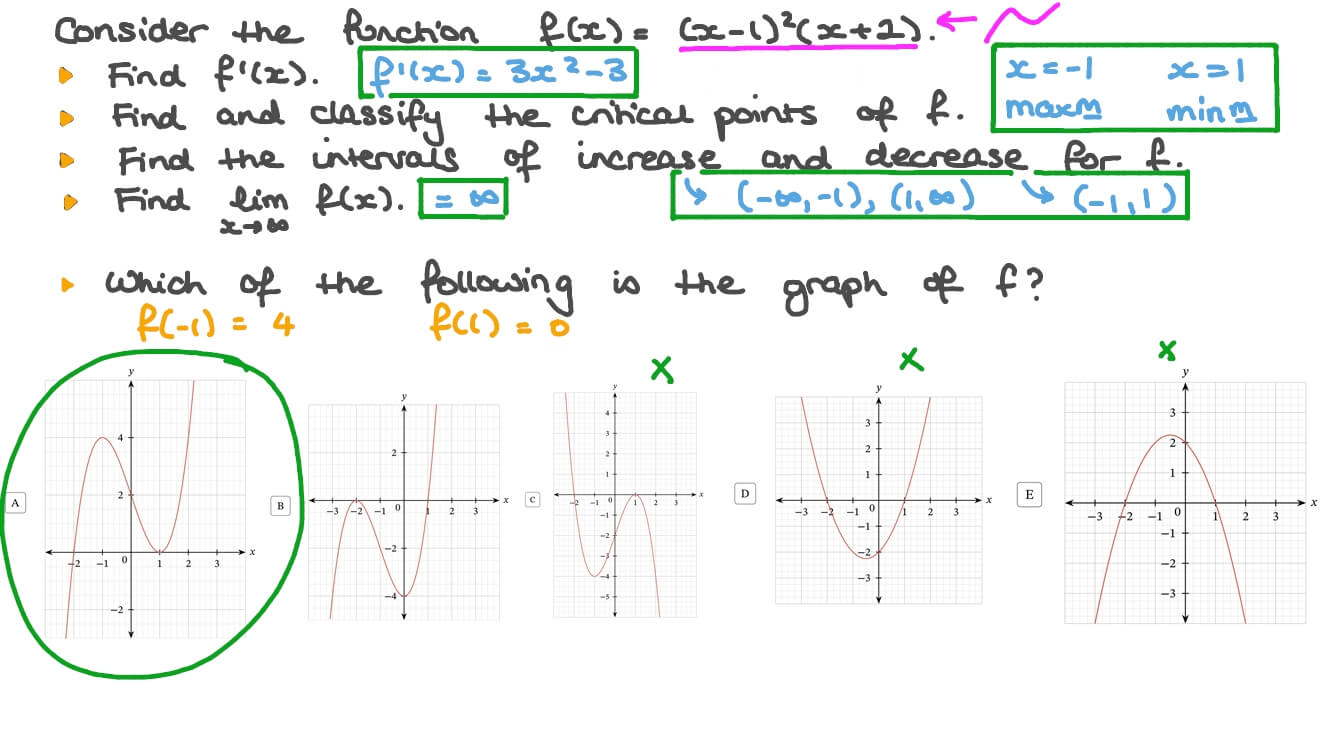



Question Video Graphing Using Derivatives Of Given Functions Nagwa




Theorem For Limits Of Composite Functions Video Khan Academy



Division By Zero Wikipedia
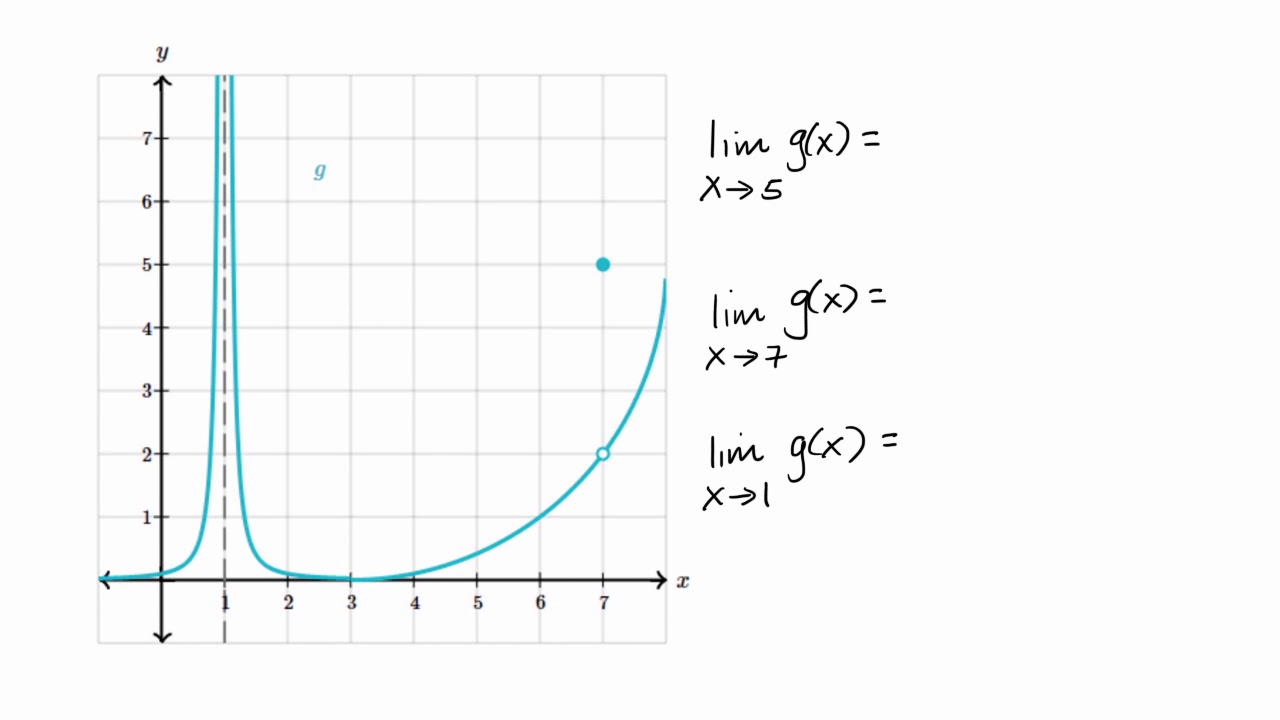



Estimating Limit Values From Graphs Video Khan Academy
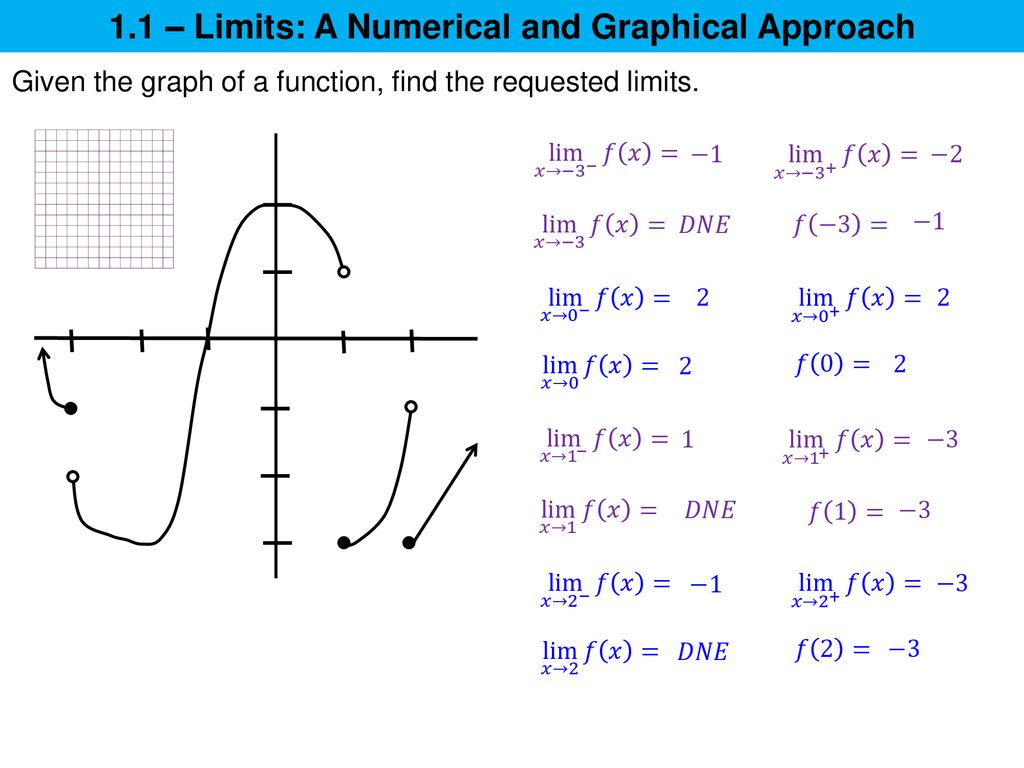



1 1 Limits A Numerical And Graphical Approach Ppt Download
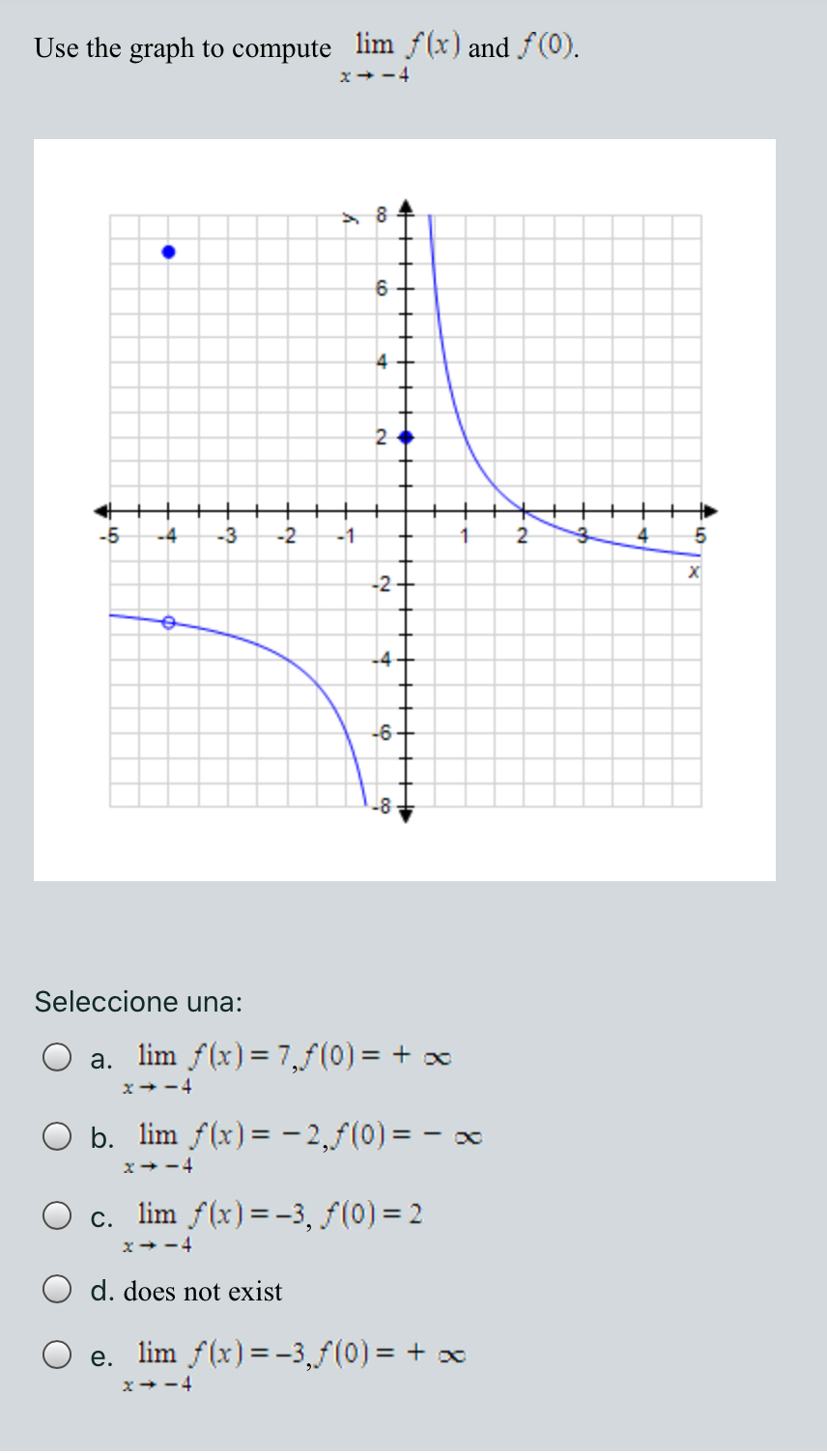



Solved Use The Graph To Compute Lim F X And F O X Chegg Com




The Graph Of The Function F X X Sin 21x 0 Sx S1 Is Shown Below Define F X F X Fn 1 X F F X For N 21 1 Y X Y F X




Find Lim Limits N To Infty Int 0 1 F N X Dx With F 0 X X And F N 1 X Sin Pi F N X Mathematics Stack Exchange



Free Essays Homework Help Flashcards Research Papers Book Reports Term Papers History Science Politics
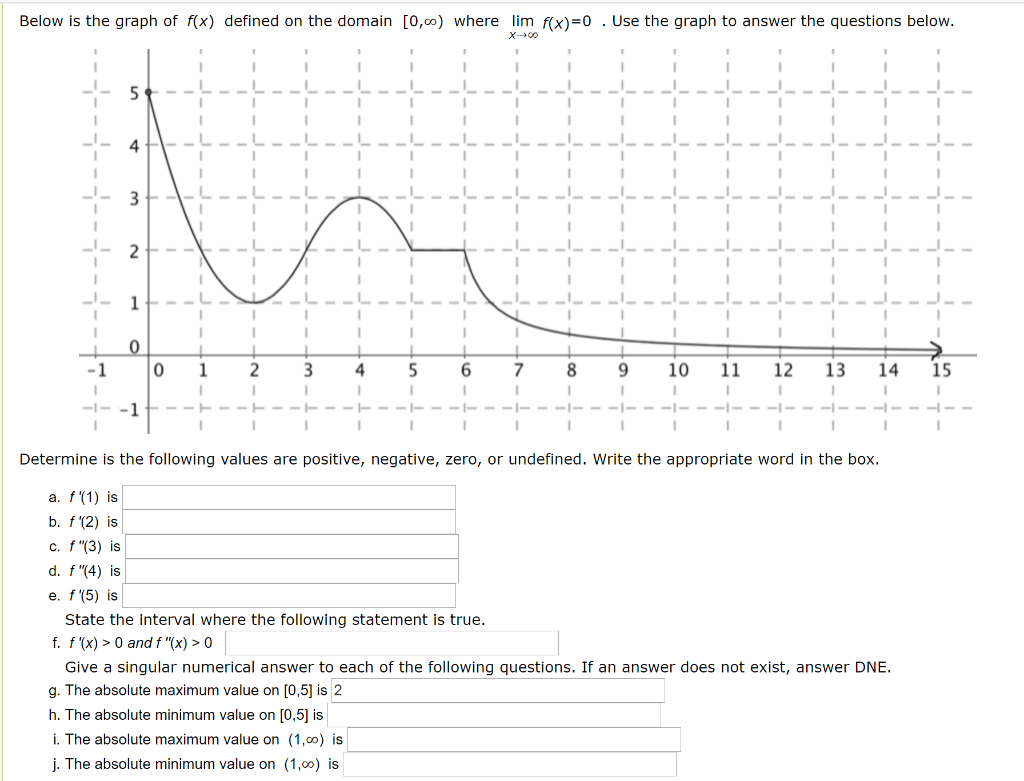



Solved Below Is The Graph Of F X Defined On The Domain Chegg Com
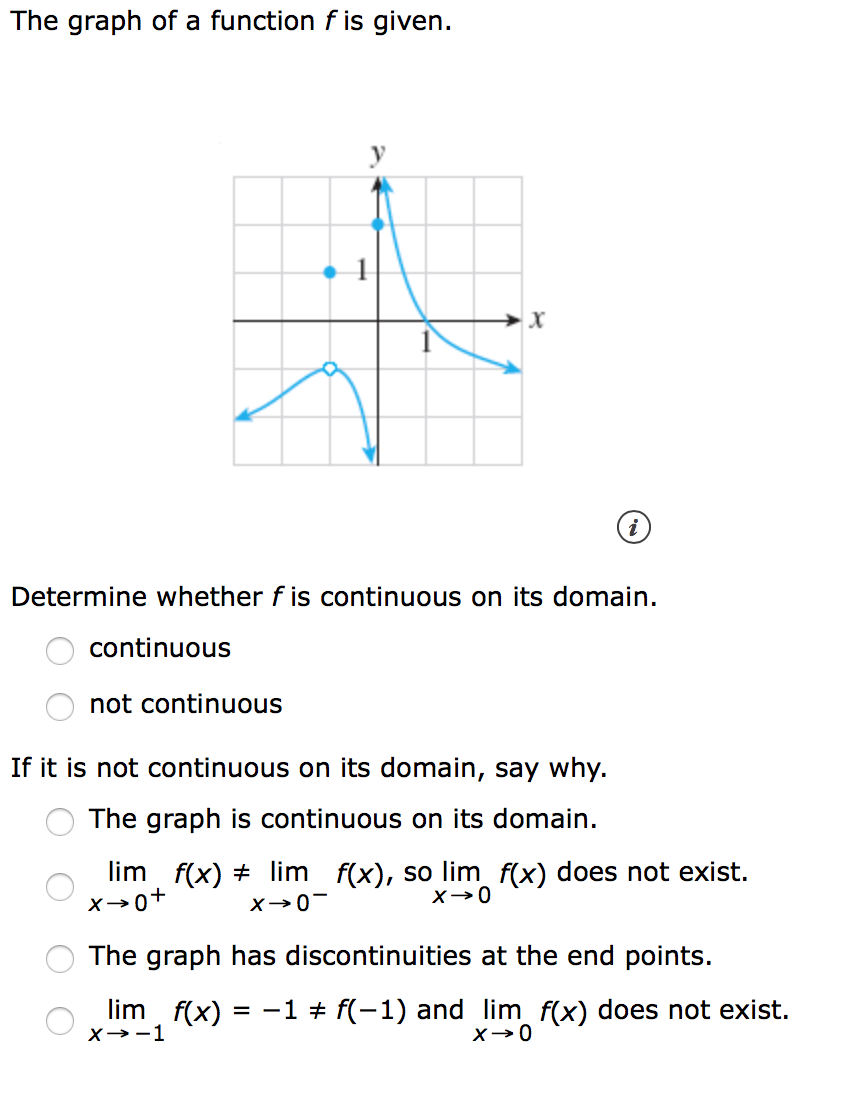



Answered The Graph Of A Function F Is Given Bartleby
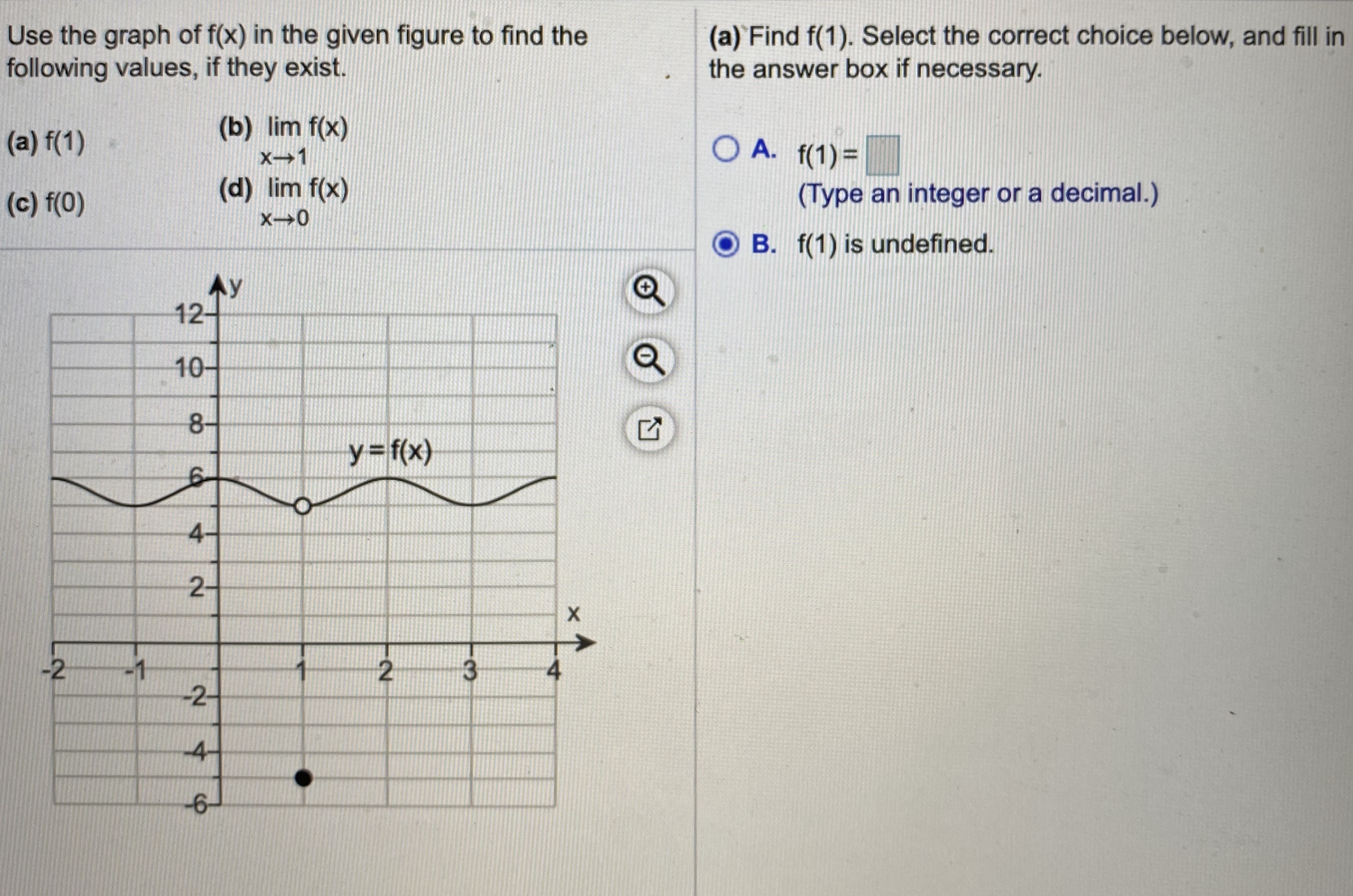



Answered Jse The Graph Of F X In The Given Bartleby




Find An Expression For The Area Under The Graph Of F As A Limit F X 5x Cos 5x 0 X P 2 Youtube




Connecting Limits At Infinity Notation And Graph Video Khan Academy
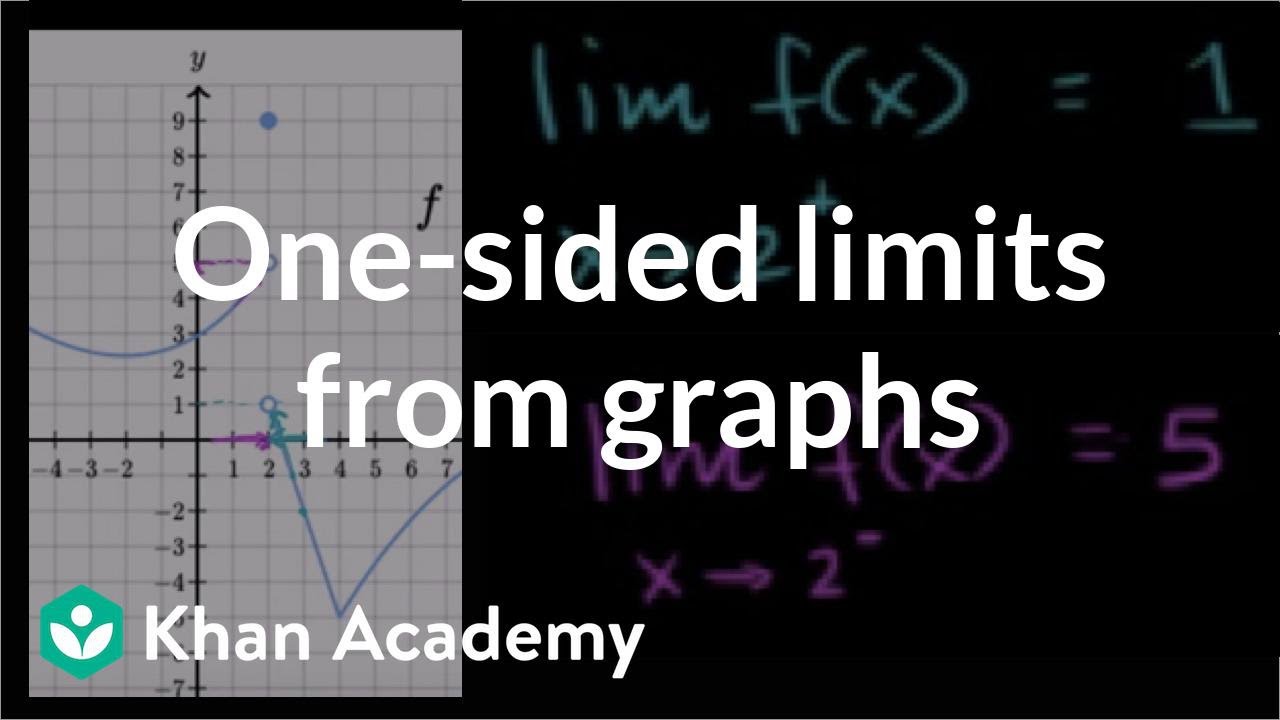



One Sided Limits From Graphs Video Khan Academy
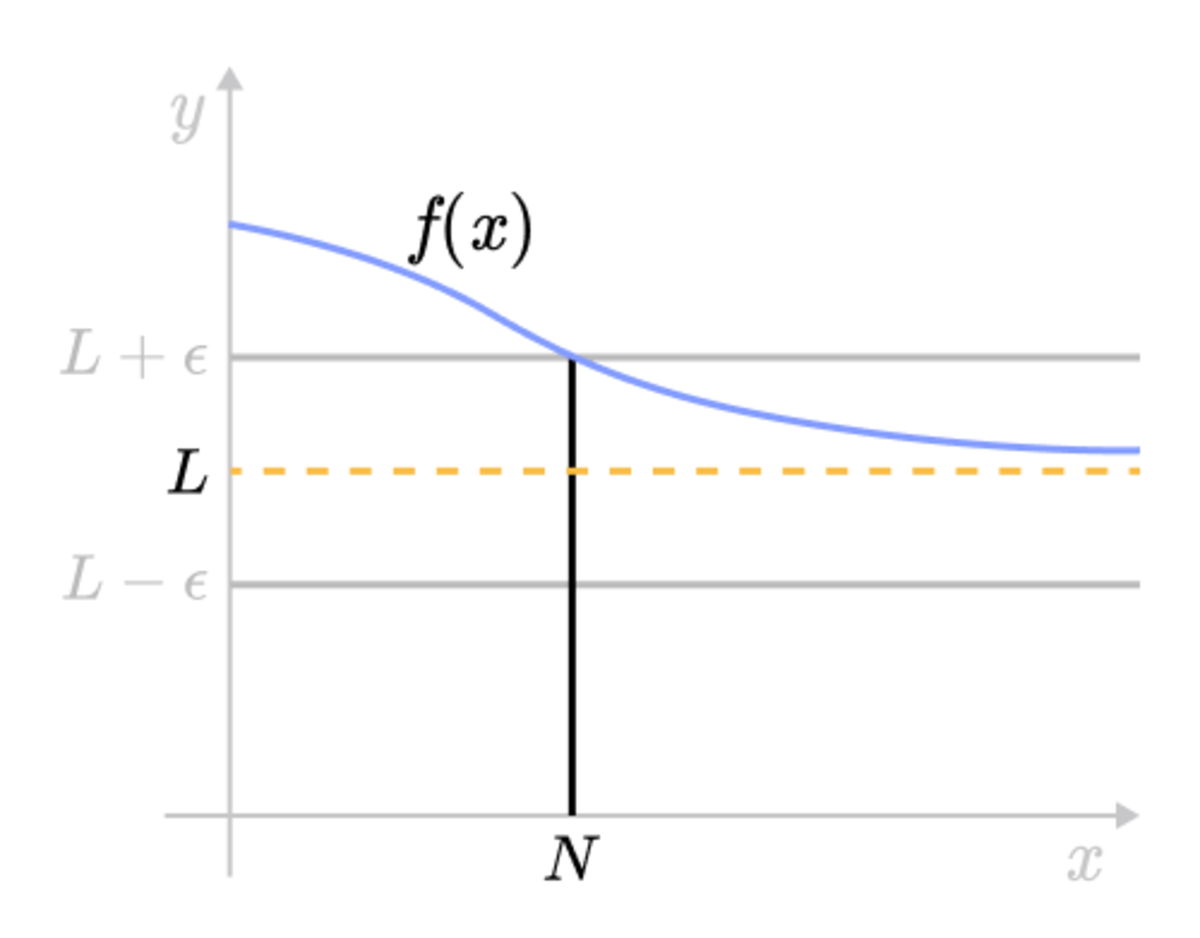



Epsilon Delta Definition Of A Limit Brilliant Math Science Wiki
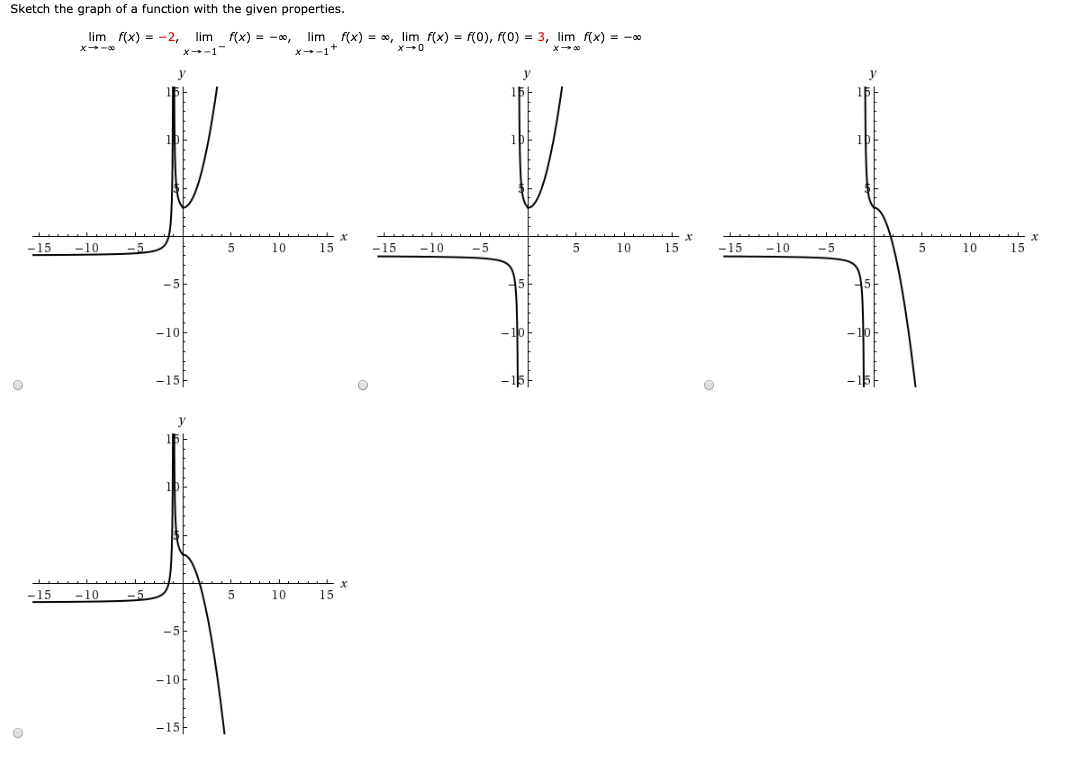



Solved Sketch The Graph Of A Function With The Given Prop Chegg Com
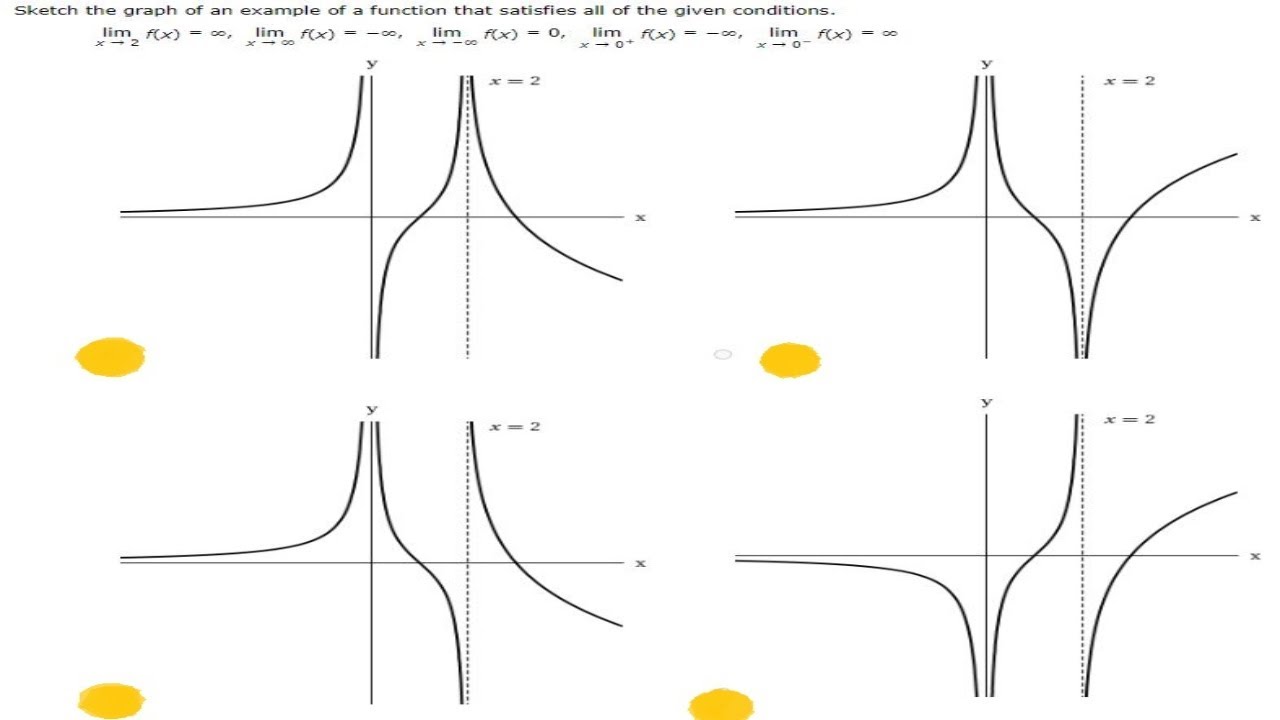



Sketch The Graph Of An Example Of A Function That Satisfies The Given Conditions Limx 2f X Youtube




Sketch Graph Of The Function From Given Conditions Youtube



No comments:
Post a Comment